ระบบตัวเลขดิจิตอล
เลขฐานสิบประกอบด้วยสัญลักษณ์ตัวเลขสิบตัว
ได้แก่ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ซึ่งมาจากความจริงที่ว่ามนุษย์มีนิ้วมืออยู่สิบนิ้ว
คำว่า “Digit” มาจากภาษาลาตินที่หมายถึง “Finger”
ตัวอย่างที่ 1 พิจารณาตัวเลข 453 เราทราบว่าเลข 4 แทนจำนวนสี่ร้อย
เลขห้าแทนจำนวน ห้าสิบ ส่วนเลข 3 แทนจำนวนสาม ตัวเลข 4
ในที่นี้มีน้ำหนักสูงสุด เรียกว่าเป็นเลขที่มีนัยสำคัญสูงสุด (Most
Significant digit: MSD) ในขณะที่เลข 3 มีน้ำหนักน้อยที่สุด (Least
Significant Digit: LSD)ตัวอย่างที่ 2 ตัวเลข 27.35 เท่ากับ โดยที่เราใช้จุดทศนิยม (Decimal point) ในการแบ่งจำนวนเต็มและเลขเศษส่วน
ตัวอย่างที่ 3 ตัวเลข 2745.214 สามารถเขียนน้ำหนักของเลขแต่ล่ะหลักในรูปของเลขสิบยกกำลังได้ดังนี้
สรุปได้ว่าโดย ทั่วๆไปแล้ว จำนวนก็คือผลบวกของผลคูณระหว่างตัวเลขกับน้ำหนักหลักของตัวเลขนั้นๆ ดังรูปที่ 2
ตัวอย่างการบวกเลขฐานสิบสองจำนวน
เช่น 99+1 จะได้ว่า
99
+
1
100
เราจะสามารถเขียนหลักการบวกเลขได้ดังนี้
สมมุติว่าเลขจำนวนหนึ่งมี
5 หลัก คือ a2a1a0.a-1a-2
โดยที่
 คือค่า สัมประสิทธิ์ที่ตำแหน่ง n และ R คือเลขฐาน
คือค่า สัมประสิทธิ์ที่ตำแหน่ง n และ R คือเลขฐาน1. จำนวนสูงสุดของตัวเลขในแต่ละหลัก จะเท่ากับ (R-1) เช่น (10-1) = 9 สำหรับเลขฐานสิบ
2. เมื่อบวกตัวเลขสูงสุดของเลขฐานนั้นๆ เช่น (10-1) ด้วย 1 จะเกิดการทด (Carry)
3. ผลลัพธ์ 99+1 คือ 100 จะเห็นได้ว่าตัวเลขเดียวกันแต่อยู่ในหลักที่ต่างกันจากซ้ายไปขวา ตัวเลขในหลักนั้นจะมีค่าเป็น R เท่าของหลัก ถัดไป เช่น เลข 1 ในหลักร้อยก็จะมีค่าเป็นสิบเท่าของเลข 1 ในหลักสิบ
เลขฐานสิบไม่เหมาะสมต่อการนำมาใช้งานในระบบดิจิตอล เนื่องจากการสร้างวงจรอิเล็กทรอนิกส์ที่สามารถทำงานกับระดับแรงดันไฟฟ้าสิบ ระดับได้อย่างแม่นยำนั้น ทำได้ยาก ในขณะที่การออกแบบวงจรให้ทำงานกับระดับแรงดันสองระดับนั้น กระทำได้ง่ายกว่ามาก
ระบบเลขฐานสอง (Binary system)
จำนวนในเลขฐานสองมีได้เพียงสองค่าคือ เลข “0” และ “1” เรียกว่า บิต(bit) ตัวเลขฐานสองสามารถแทนจำนวนในเลขฐานสิบหรือฐานอื่นได้โดยการเพิ่มจำนวนหลัก ให้เพียงพอ
ในรูปที่ 3 แสดงตัวอย่างตัวเลขฐานสอง 1011.101 ตัวเลขที่อยู่ทางหน้าจุดไบนารี่จะมีค่าเป็นสองยกกำลังจำนวนบวก ส่วนตัวเลขที่อยู่หลังจุดไบนารี่จะมีค่าเป็นสองยกกำลังค่าลบ ใน
การแปลงเลขฐานสองเป็นเลขฐานสิบ
สามารถทำได้ง่ายๆดังนี้
จุดสังเกต ตัวห้อย 2 และ10 ใช้แทนเลขฐานของจำนวนที่เราพิจารณา
ในระบบตัวเลขฐานสองตัวเลขในหลักต่างๆมักนิยมเรียกว่า บิต (Bit) จากในรูปที่สาม จะแสดงให้เห็นว่ามีตัวเลขสี่บิตอยู่หน้าจุดไบนารี่ที่แทนจำนวนเต็มและมีตัว เลขสามบิตหลังจุดไบนารี่ที่แทนเลขเศษส่วน บิตที่ทางซ้ายมือสุดจะเป็นบิตที่มีนัยสำคัญสูงสุด (Most Significant Bit: MSB) ส่วนบิตที่อยู่ทางขวามือสุดเป็นบิตที่มีนัยสำคัญต่ำที่สุด (Least Significant Bit: LSB)
ตัวอย่างที่ 4 ตัวเลขฐานสองแปดบิตจะแทนจำนวนสูงสุดในตัวเลขฐานสิบได้เท่ากับเท่าใด
คำตอบ
การแสดงจำนวนเลขฐานสอง
ในระบบดิจิตอล ข้อมูลที่จะถูกประมวลผลมักอยู่ในรูปของจำนวนตัวเลขฐานสอง ซึ่งจำนวนในเลขฐานสองสามารถแทนได้ด้วยอุปกรณ์ใดๆที่มีการทำงานเพียงสองสถานะ เช่น สวิตช์ที่เปิดวงจรแทน “0” หรือสวิตช์ปิดวงจรแทน “1” ในรูปที่ 4a แสดงตัวอย่างการแทนจำนวนเลขสอง 100102 ด้วยสวิตช์เปิดปิดห้าตัว ส่วนในรูป 4b ใช้การเจาะรูหรือไม่เจาะรูบนกระดาษแทนเลขฐานสอง
นอกจากนี้ ยังมีอุปกรณ์อีกหลายชนิดที่มีสภาวะการทำงานสองสถานะที่ต่างกันมาก ซึ่งสามารถแทนจำนวนฐานสองได้เช่น หลอดไฟ (ดับ หรือ สว่าง) ไดโอด (นำกระแส หรือ ไม่นำกระแส) ขดลวดรีเลย์ (จ่ายไฟ หรือ ไม่จ่ายไฟ) ทรานซิสเตอร์ (คัตออฟ หรือ อิ่มตัว) โฟโต้เซลล์ (ได้รับแสง ไม่ได้รับแสง) เทอร์โมสตัต (เปิด หรือปิด วงจร) จุดบนแถบบันทึกแม่เหล็ก (ไม่อำนาจแม่เหล็กหรือไม่มี) เป็นต้น
การแปลงเลขฐานสิบเป็นเลขฐานสอง
มี 2 วีธี คือ วิธีการลบและวิธีการหาร
วิธีการลบ
ทำได้โดยนำค่ากำลังของสองค่าสูงสุดที่สามารถลบค่า เลขฐานสิบได้ไปลบ จากนั้นแทนค่าบิตนี้เป็นค่า “1” และ เป็นบิตสูงสุด เศษที่ได้จากการลบให้นำค่าสองยกกำลัง ค่าที่ต่ำลงมาไปลบ ถ้าลบให้ได้เป็น “1” และลบต่อไปเรื่อย ๆ ถ้าลบไม่ได้ให้เป็น “0”และนำค่าสองยกกำลังต่ำลงมาไปลบแทน
ตัวอย่าง การแปลงเลข 4910 เป็นเลขฐานสองทำได้ดังนี้
วิธีการหาร
วิธีนี้จะนำฐานสิบมาหารด้วยสองไปเรื่อยๆ และนำเศษที่เหลือมาเขียนเป็นเลขฐานสอง โดยค่าแรกจะเป็นบิตต่ำ และนำผลหารที่ได้มาหารด้วยสองต่อไป
ตัวอย่าง การแปลงเลข 4910 เป็นเลขฐานสองทำได้ดังนี้
49 / 2 = 24 เหลือเศษ 1 (บิตต่ำสุด)
24 / 2 = 12 เหลือเศษ 0
12 / 2 = 6 เหลือเศษ 0
6 / 2 = 3 เหลือเศษ 0
3 / 2 = 1 เหลือเศษ 1
1 / 2 = 0 เหลือเศษ 1 (บิตสูงสุด)
นำเศษที่ได้มาเขียนเป็นเลขฐานสองจะได้เป็น 1 1 0 0 0 1
ระบบเลขฐานแปด
ระบบเลขฐานแปดนี้จะใช้สัญลักษณ์แทน 8 ตัว คือ 0,1,2,3,4,5,6 และ 7 การแปลงเลขฐานแปด เป็นเลขฐานสิบทำได้โดยนำค่าแต่ละหลักคูณกับ ค่าน้ำหนักของแต่ละหลัก
ตัวอย่าง การแปลงเลขฐานแปดเป็นเลขฐานสิบ
ระบบเลขฐานสิบหก
ระบบเลขฐานสิบหกนี้จะใช้สัญลักษณ์แทน 16 ตัว คือ 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E และ F เลขฐานสิบหกหนึ่งหลักสามารถ
แทนเลขฐานสองได้ 4 หลัก
การแปลงเลขฐานสิบหกเป็นเลขฐานสอง
สามารถทำได้โดยแทนเลขฐานสิบหกแต่ละหลักด้วยเลขฐานสอง 4 บิต และนำมาเรียงต่อกัน
9F2H = 9 F 2
= 1001 1111 0010
= 100111110010
ส่วนการแปลงเลขฐานสองเป็นเลขฐานแปด
สามารถทำได้โดยให้จัดกลุ่มครั้งละ 4 บิต และแทนเลขฐานสองแต่ละกลุ่มด้วยเลขฐานสิบหก
11010101 = 1101 0101
= D 5
= D5H
การแปลงเลขฐานสิบหกเป็นเลขฐานสิบ
สามารถทำได้โดยน้ำหนักของเลขฐานสิบหก แต่ละหลักจะเป็น 160,161,162 …… ไปคูณกับค่าแต่ละหลัก แล้วนำมาบวกกัน
A0916 =10 x 162 + 0 x 161 + 9 x 160
=2560 + 9
=2569
การแปลงเลขฐานสิบเป็นเลขฐานสิบหก
สามารถทำได้โดยการหารด้วย 16 ไปเรื่อย ๆ
418 / 16 = 26 เศษ 2
26 / 16 = 1 เศษ 10=A
1 / 16 = 0 เศษ 1
418 = 1A2





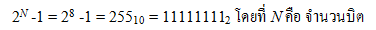





ไม่มีความคิดเห็น:
แสดงความคิดเห็น